Question

A train traveling at 25 m/s is blowing its whistle at 440 Hz as it crosses a level crossing. You are waiting at the crossing and hear the pitch of the whistle change as the train passes you. The sound you hear changes from a frequency of to a frequency of _ _(Take the speed of sound to be 340 m/s.)

a. 410 Hz, 475 Hz
b. 472 Hz, 408 Hz
c. 408 Hz, 472 Hz
d. 475 Hz, 410 Hz

Answer 1

b) 472HZ, 408HZ

Step-by-step explanation:

To find the frequencies perceived when the bus approaches and the train departs, you use the Doppler's effect formula for both cases:

`f_o=f(v_s+v_o)/(v_s-v)\\\\f_o=f'(v_s-v_o)/(v_s+v)\\\\`

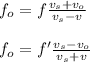
fo: frequency of the source = 440Hz

vs: speed of sound = 343m/s

vo: speed of the observer = 0m/s (at rest)

v: sped of the train

f: frequency perceived when the train leaves us.

f': frequency when the train is getTing closer.

Thus, by doing f and f' the subjects of the formulas and replacing the values of v, vo, vs and fo you obtain:

`f=f_o(v_s-v)/(v_s+v_o)=(440Hz)(340m/s-25m/s)/(340m/s)=408Hz\\\\f'=f_o(v_s+v)/(v_s-v_o)=(440Hz)(340m/s+25m/s)/(340m/s)=472Hz`

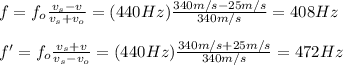
hence, the frequencies for before and after tha train has past are

b) 472HZ, 408HZ