Question

Last year, 50% of MNM, Inc. employees were female. It is believed that there has been a reduction in the percentage of females in the company. This year, in a random sample of 400 employees, 180 were female.

Based on this information, you want to determine if there has been a decrease in the percentage of females in the company (at the significance level of 5%). Round your solutions for this Exhibit to 4 decimal places.

Answer 1

We conclude that there has been a decrease in the percentage of females in the company from last year.

Explanation:

We are given that Last year, 50% of MNM, Inc. employees were female. It is believed that there has been a reduction in the percentage of females in the company.

This year, in a random sample of 400 employees, 180 were female.

Let p = percentage of females in the company this year.

So, Null Hypothesis,
`H_0` : p
`\geq` 50% {means that there has not been a decrease in the percentage of females in the company from last year}

Alternate Hypothesis,
`H_A` : p < 50% {means that there has been a decrease in the percentage of females in the company from last year}

The test statistics that will be used here is One-sample z proportion statistics;

T.S. =
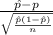`\frac{\hat p-p}{{\sqrt{(\hat p(1-\hat p))/(n) } } } }` ~ N(0,1)

where,
`\hat p` = proportion of female in a sample of 400 employees =
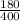`(180)/(400)` = 0.45

n = sample of employees = 400

So, test statistics =
`\frac{0.45-0.50}{{\sqrt{(0.45(1-0.45))/(400) } } } }`

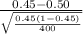
= -2.0101

The value of the test statistics is -2.0101.

Now at 5% significance level, the z table gives critical value of -1.6449 for left-tailed test. Since our test statistics is less than the critical value of z as -2.0101 < -1.6449, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that there has been a decrease in the percentage of females in the company from last year.