Answer:
a) Therefore, the minimum number of bits required is 6.
b) Therefore, we can admit 4 more students to the class without requiring additional bit for each student's unique bit pattern
Step-by-step explanation:
a) The number of unique bit patterns using n bits is calculated using
 .
.
In this case, there are 60 students, so, we need at least 60 unique bit pattern.
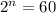
Where n is the number of bit required; we are to find n
We take the logarithm of both side:
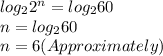
Therefore, the minimum number of bits required is 6
b) How many more students can be admitted to the class without requiring additional bits for each student's unique bit pattern?
With 6 bits, we can represent up to
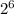 unique bit pattern which is 64 unique bit patterns.
unique bit pattern which is 64 unique bit patterns.
To get the number of additional bit:
64 - 60 = 4
Therefore, we can admit 4 more students to the class without requiring additional bit for each student's unique bit pattern