Question

asked Jul 18, 2021 183k views

1 Answer

Omid Shagiwal · Answer 1 · 2021-07-23T01:53:55+0000

Answer:

(a) The probability that the sample average sediment density is at most 3.00 is 0.092.

The probability that the sample average sediment density is between 2.70 and 3.00 is 0.477.

(b) The sample size must be at least 77.

Explanation:

The random variable X ca be defined as the sediment density (g/cm) of a specimen from a certain region.

The random variable X is normally distributed with mean, μ = 2.7 and standard deviation, σ = 0.75.

(a)

A random sample of n = 25 specimens is selected.

Compute the probability that the sample average sediment density is at most 3.00 as follows:

Apply continuity correction:

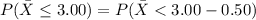
$P(\bar X\leq 3.00)=P(\bar X<3.00-0.50)$

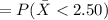
$=P(\bar X<2.50)\\$

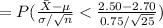
$=P((\bar X-\mu)/(\sigma/√(n))<(2.50-2.70)/(0.75/√(25)))$

$=P(Z<-1.33)\\=1-P(Z<1.33)\\=1-0.90824\\=0.09176\\\approx0.092$

Thus, the probability that the sample average sediment density is at most 3.00 is 0.092.

Compute the probability that the sample average sediment density is between 2.70 and 3.00 as follows:

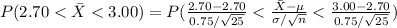
$P(2.70<\bar X<3.00)=P((2.70-2.70)/(0.75/√(25))<(\bar X-\mu)/(\sigma/√(n))<(3.00-2.70)/(0.75/√(25)))$

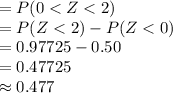
$=P(0<Z<2)\\=P(Z<2)-P(Z<0)\\=0.97725-0.50\\=0.47725\\\approx0.477$

*Use a z-table.

Thus, the probability that the sample average sediment density is between 2.70 and 3.00 is 0.477.

(b)

It is provided that:

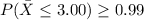
$P(\bar X\leq 3.00)\geq 0.99$

$P(\bar X<2.50)\geq 0.99$

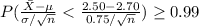
$P((\bar X-\mu)/(\sigma/√(n))<(2.50-2.70)/(0.75/√(n)))\geq 0.99$

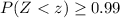
$P(Z<z)\geq 0.99$

The value of z for the probability above is

z ≥ 2.33

Compute the value of n as follows:

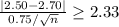
$(|2.50-2.70|)/(0.75/√(n))\geq 2.33$

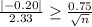
$(|-0.20|)/(2.33)\geq (0.75)/(√(n))$

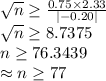
$√(n)\geq (0.75* 2.33)/(|-0.20|)\\√(n)\geq 8.7375\\n\geq 76.3439\\\approx n\geq 77$

Thus, the sample size must be at least 77.

Please log in or register to add a comment.