There is an error in the first sentence of the question; the right format is:
Suppose a 500.mL flask is filled with 1.9mol of NO3 and 1.6mol of NO2.
It should be NO2 and not NO.
Answer:
The equilibrium molarity of NO = 0.21695 m
Step-by-step explanation:
Given that :
the volume = 500 mL = 0.500 m
number of moles of
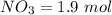
number of moles of
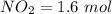
Then we can calculate for their respectively concentrations as :
![[NO_3] = (number \ of \ moles)/(volume)](https://img.qammunity.org/2021/formulas/chemistry/college/6jbvi3fkonzdf7rufi14ocbv7e1qg12ljq.png)
![[NO_3] = (1.9)/(0.500)](https://img.qammunity.org/2021/formulas/chemistry/college/7n5xyetfl3lmf7tf5lrb5898hnnnw020z6.png)
![[NO_3] = 3.8 \ M](https://img.qammunity.org/2021/formulas/chemistry/college/ek9gm1vsz9wno9u6x5xhy2z2kyyrym2jhw.png)
![[NO_2] = (number \ of \ moles)/(volume)](https://img.qammunity.org/2021/formulas/chemistry/college/sk78tqaqfyax4qp455a3rh4s658ua2w6h0.png)
![[NO_2] = \frac{}{} (1.6)/(0.500)](https://img.qammunity.org/2021/formulas/chemistry/college/qtff5j5xq3d68rh6ea6y2o8hfealpremuq.png)
![[NO_2] = 3.2 \ M](https://img.qammunity.org/2021/formulas/chemistry/college/tu2vvjpmr5u11bkvjv8zr6xe57df3e6t90.png)
The chemical reaction can be written as:
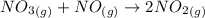
The ICE table is as follows;
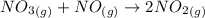
Initial 3.8 - 3.2
Change +x x -2x
Equilibrium 3.8+x +x 3.2 - 2x
![K_c=([NO_2]^2)/([NO_3][NO])](https://img.qammunity.org/2021/formulas/chemistry/college/p9w4kedx91xxbagz34jkt34qgtes0f1q9b.png)
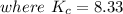


Using quadratic formula;
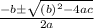
=
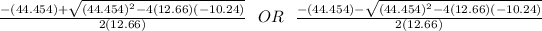
= 0.21695 OR -3.7283
Going by the positive value;
x = 0.21695
![[NO_3] = 3.8 +x = 3.8 + 0.21695](https://img.qammunity.org/2021/formulas/chemistry/college/nrvgv87ho7ysnh9o5ev1zrt6a4wc73xnfg.png)
= 4.01695 m
[NO] = x = 0.21695 m
![[NO_2] = 3.2 +x = 3.2 + 0.21695](https://img.qammunity.org/2021/formulas/chemistry/college/d5depo8nd1017cz0yzcf9uypopdv9e3ufl.png)
= 3.41695 m