Question

A long solenoid has a diameter of 12.0 cm. When a current i exists in its windings, a uniform magnetic field vector B = 36.0 mT is produced in its interior. By decreasing i, the field is caused to decrease at the rate of 7.10 mT/s. Calculate the magnitude of the induced electric field at the following distances from the axis of the solenoid.

(a) 1.60 cm and (b) 10.0 cm from the axis of the solenoid.

Answer 1

a) 3.195*10^{-3}N/C

b) 5.11*10^{-4}N/C

Step-by-step explanation:

a) to find the induced electric field for different distances you use the following formula:

`\int\vec{E}\cdot d\vec{r}=-(d\Phi_B)/(dt)\\\\E(2\pi r)=-(d\Phi_B)/(dt)\\\\E=-(1)/(2\pi r)(d\Phi_B)/(dt)`

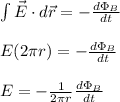
the area of the solenoid is constant, hence:

`E=-(1)/(2\pi r)\pi R^2(dB)/(dt)=-(1)/(2r)R^2(dB)/(dt)`

where you have assumed that the electric field is perpendicular to the vector of the path integral.

r: distance in which the induced electric field is measured

R: radius of the solenoid = 0.12m

dB/dt: change in the magnetic field: -7.10mT/=-7.1*10^{-3}T/s

a) for r=1.60cm=0.016m you obtain:

`E=-(1)/(2(0.016m))(0.12m)^2(-7.1*10^(-3)T/s)=3.195*10^(-3)N/C`

b) for r=10.0cm=0.10m

`E=-(1)/(2(0.10m))(0.12m)^2(-7.1*10^(-3)T/s)=5.11*10^(-4)N/C`