Question

(Hypothetical.) Suppose five measurements of the volume of a liquid yield the following data (in milliliters).

52 48 49 52 53

Assume that the different measurements are due only to measurement error, and that measurement error is Normally distributed. The goal is to set up an approximate 95% confidence interval for the correct measurement. In each part, answer correct to three decimal places.

First find the average and SD of the data.

Answer 1

The 95% confidence interval for the measurements is [48.106, 53.494].

Explanation:

The average M of this sample is

`M=(1)/(5)\sum_(i=1)^5x_i=(1)/(5)(52+48+49+52+53)\\\\\\M=(254)/(5)=50.800`

The standard deviation s of this sample is

`s=\sqrt{(1)/((n-1))\sum_(i=1)^5(x_i-M)^2}`

`s=\sqrt{(1)/(4)\cdot [(52-50.8)^2+(48-50.8)^2+(49-50.8)^2+(52-50.8)^2+(53-50.8)^2]}`

`s=\sqrt{(1)/(4)\cdot [(1.44)+(7.84)+(3.24)+(1.44)+(4.84)]}=\sqrt{(18.8)/(4)}=√(4.7)\\\\\\s=2.168`

The degrees of freedom are

`df=n-1=5-1=4`

Then, the critical value of t for a 95% CI and 4 degrees of freedom is t=2.776.

The margin of error of the CI is:

`E=t\cdot s/√(n)=2.776\cdot 2.17/√(5)=6.024/2.236=2.694`

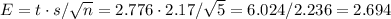
Then, the lower and upper bounds of the CI are:

`LL=50.800-2.694=48.106\\\\UL=50.800+2.694=53.494`

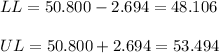
The 95% confidence interval for the measurements is [48.106, 53.494].