Question

A construction company has an expenditure rate of E'(x)=e^(0.17 x) dollars per day on a particular paving job and an income rate of I'(x)=116.2 - e^(.17x) dollars per day on the same​ job, where x is the number of days from the start of the job. The​ company's profit on that job will equal total income less total expenditures. Profit will be maximized if the job ends at the optimum​ time, which is the point where the two curves meet.

(a) Find the optimum number of days for the job to last.
​(b) Find the total income for the optimum number of days.
​(c) Find the total expenditures for the optimum number of days.
​(d) Find the maximum profit for the job.

Answer 1

a) optimum number of days for the job to last = 24 days

b) Total income for the optimum number of days = $2434.83

c) Total expenditures for the optimum number of days = $341.77

d) Maximum profit for the job = $2093.06

Explanation:

a) Expenditure rate ,
`E'(x) = e^(0.17x)`

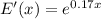
Income rate
`I'(x) = 116.2-e^(0.17x)`

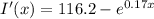
The job lasts for many days where the income is more than expenditure and job ends when both are equal.

The optimum number of days is the value of x where I'(x) = E'(x)

`116.2-e^(0.17x) =e^(0.17x)\\116.2=2e^(0.17x)\\58.1=e^(0.17x)\\ {0.17x} = ln(58.1)`

`x = ln(58.1)/0.17\\x = 23.9`

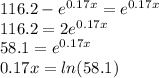
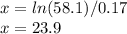
The optimum number of days for the job to last is 24 days

b)
`I'(x) = 116.2-e^(0.17x)`

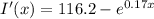
Integrating both sides in the equation above:

`I(x) = 116.2x-(e^(0.17x)/0.17)`

Substituting
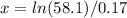`x = ln(58.1)/0.17` into the equation above , The income for the optimum number of days becomes:

`I(x) = 116.2* (ln(58.1)/0.17)-(e^(0.17(ln(58.1)/0.17))/0.17)I(x) = (116.2* (ln(58.1)/0.17))-(58.1)/0.17)I(x)=2776.60 -341.76I(x) =2434.83`

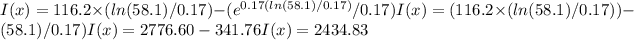
c)

`E'(x) = e^(0.17x)`

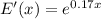
Integrating the equation above:

`E(x) = (1/0.17)e^(0.17x)`

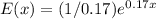
Substituting
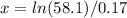`x = ln(58.1)/0.17` into the above equation, expenditure for the optimum number of days is;

`E(x) =1/(0.17)e^(0.17(ln(58.1)/0.17)) \\E(x) =58.1/0.17\\E(x)=341.77`

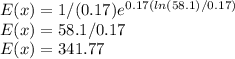
d) Maximum profit is 2434.83- 341.77=2093.06