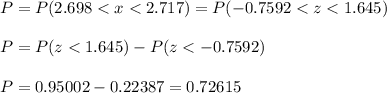Question

Find the probability and interpret the results. If​ convenient, use technology to find the probability. During a certain week the mean price of gasoline was ​$2.7042.704 per gallon. A random sample of 3131 gas stations is drawn from this population. What is the probability that the mean price for the sample was between ​$2.6982.698 and ​$2.7172.717 that​ week? Assume sigmaσequals=​$0.0440.044.

Answer 1

The probability that the mean price for the sample was between ​$2.6982.698 and ​$2.7172.717 that​ week is P=0.726.

Explanation:

We have a population mean price of $2.704. The standard deviation is $0.044.

We draw a sample of size n=31 out of this population.

We have to calculate the probability that the mean price for this sample is between ​$2.698 and ​$2.717 that​ week.

To calculate this, first we calculate the z-scores for both values:

X1=2.698

`z_1=(X_1-\mu)/(\sigma/√(n))=(2.698-2.704)/(0.044/√(31))=(-0.006)/(0.0079)=-0.7592`

X2=2.717

`z_2=(X_2-\mu)/(\sigma/√(n))=(2.717-2.704)/(0.044/√(31))=(0.013)/(0.0079)=1.645`

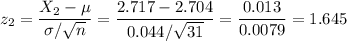
Then, we have:

`P=P(2.698<x<2.717)=P(-0.7592<z<1.645)\\\\P=P(z<1.645)-P(z<-0.7592)\\\\P=0.95002-0.22387=0.72615`