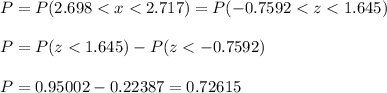Answer:
The probability that the mean price for the sample was between $2.6982.698 and $2.7172.717 that week is P=0.726.
Explanation:
We have a population mean price of $2.704. The standard deviation is $0.044.
We draw a sample of size n=31 out of this population.
We have to calculate the probability that the mean price for this sample is between $2.698 and $2.717 that week.
To calculate this, first we calculate the z-scores for both values:
X1=2.698
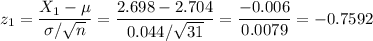
X2=2.717
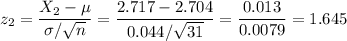
Then, we have: