Question

Help ASAP Please(Answered)

Among 320 randomly selected airline travelers, the mean number of hours spent travelling per year is 24 hours and the standard deviation is 2.9. What is the margin of error, assuming a 90% confidence level?

Remember:

90% confidence level = z-score of 1.645

Margin of error, ME, can be determined using the formula ,ME= Z*S/ square root of N



0.27<---- This was the answer for others who look at this problem


3.12


0.25


0.70

Answer 1

The margin of error is 0.267

Explanation:

In this question, we are tasked with calculating the margin of error for the data in the question.

To calculate the margin of error, we employ a mathematical formula.

Mathematically,

the margin of error =
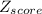`Z_(score)` × s/√n

Where z is the z-score at the confidence interval obtained from the table of standard score values, s is the standard deviation while n is the number of elements in the population

The values are;

z-score at 90% C.I = 1.645

s = 2.9

n = 320

Let's plug these values as follows;

margin of error = 1.645 × 2.90/√320 = 1.645 × 2.90/17.89 = 1.645 × 0.1621017 = 0.267