Question

If a random sample of 30 homes south of Center Street in Provo has a mean selling price of $145,000 and a standard deviation of $4750, and a random sample of 28 homes north of Center Street has a mean selling price of $148,325 and a standard deviation of $5750, can you conclude that there is a significant difference between the selling price of homes in these two areas of Provo at the 0.05 level.

(a) Find t. (Give your answer correct to two decimal places.)(b) Find the p-value. (Give your answer correct to four decimal places.)

Answer 1

(a) The value of test statistics = -2.41

(b) The P-value = 0.0097

Explanation:

We are given that a random sample of 30 homes south of Center Street in Provo has a mean selling price of $145,000 and a standard deviation of $4750, and a random sample of 28 homes north of Center Street has a mean selling price of $148,325 and a standard deviation of $5750.

Let
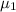`\mu_1` = mean selling price of homes south of Center Street in Provo

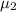`\mu_2` = mean selling price of homes north of Center Street in Provo

SO, Null Hypothesis,
`H_0` :
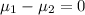`\mu_1-\mu_2=0` or
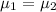`\mu_1= \mu_2` {means that there is no significant difference between the selling price of homes in these two areas of Provo}

Alternate Hypothesis,
`H_A` :
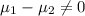`\mu_1-\mu_2\\eq 0` or
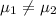`\mu_1\\eq \mu_2` {means that there is a significant difference between the selling price of homes in these two areas of Provo}

The test statistics that will be used here is Two-sample t test statistics as we don't know about the population standard deviations;

T.S. =
`\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}{s_p\sqrt{(1)/(n_1)+(1)/(n_2) } }` ~
`t__n__1+_n__2-2`

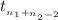
where,
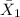`\bar X_1` = sample mean selling price of homes south of Center Street in Provo = $145,000

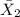`\bar X_2` = sample mean selling price of homes north of Center Street in Provo = $148,325

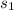`s_1` = sample standard deviation of homes south of Center Street in Provo = $4,750

`s_2` = sample standard deviation of homes north of Center Street in Provo = $5,750

`n_1` = sample of homes south of Center Street in Provo = 30

`n_2` = sample of homes north of Center Street in Provo = 28

Also,
`s_p=\sqrt{((n_1-1)s_1^(2)+(n_2-1)s_2^(2) )/(n_1+n_2-2) }` =
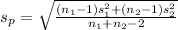`\sqrt{((30-1)* 4,750^(2)+(28-1)* 5,750^(2) )/(30+28-2) }` = 5255.95

(a) So, the test statistics =
`\frac{(145,000-148,325)-(0)}{5255.95 * \sqrt{(1)/(30)+(1)/(28) } }` ~
`t_5_6`

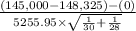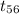
= -2.41

(b) Now, the P-value of the test statistics is given by;

P-value = P(
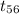`t_5_6` < -2.41) = 0.0097 {using t table}