Answer:
(a) The value of test statistics = -2.41
(b) The P-value = 0.0097
Explanation:
We are given that a random sample of 30 homes south of Center Street in Provo has a mean selling price of $145,000 and a standard deviation of $4750, and a random sample of 28 homes north of Center Street has a mean selling price of $148,325 and a standard deviation of $5750.
Let
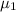 = mean selling price of homes south of Center Street in Provo
= mean selling price of homes south of Center Street in Provo
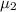 = mean selling price of homes north of Center Street in Provo
= mean selling price of homes north of Center Street in Provo
SO, Null Hypothesis,
 :
:
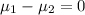 or
or
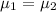 {means that there is no significant difference between the selling price of homes in these two areas of Provo}
{means that there is no significant difference between the selling price of homes in these two areas of Provo}
Alternate Hypothesis,
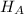 :
:
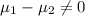 or
or
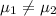 {means that there is a significant difference between the selling price of homes in these two areas of Provo}
{means that there is a significant difference between the selling price of homes in these two areas of Provo}
The test statistics that will be used here is Two-sample t test statistics as we don't know about the population standard deviations;
T.S. =
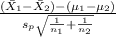 ~
~
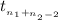
where,
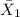 = sample mean selling price of homes south of Center Street in Provo = $145,000
= sample mean selling price of homes south of Center Street in Provo = $145,000
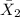 = sample mean selling price of homes north of Center Street in Provo = $148,325
= sample mean selling price of homes north of Center Street in Provo = $148,325
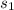 = sample standard deviation of homes south of Center Street in Provo = $4,750
= sample standard deviation of homes south of Center Street in Provo = $4,750
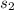 = sample standard deviation of homes north of Center Street in Provo = $5,750
= sample standard deviation of homes north of Center Street in Provo = $5,750
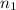 = sample of homes south of Center Street in Provo = 30
= sample of homes south of Center Street in Provo = 30
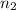 = sample of homes north of Center Street in Provo = 28
= sample of homes north of Center Street in Provo = 28
Also,
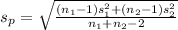 =
=
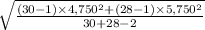 = 5255.95
= 5255.95
(a) So, the test statistics =
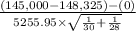 ~
~
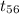
= -2.41
(b) Now, the P-value of the test statistics is given by;
P-value = P(
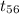 < -2.41) = 0.0097 {using t table}
< -2.41) = 0.0097 {using t table}