Question

A solid weak acid is weighed, dissolved in water and diluted to exactly 50.00 ml. 25.00 ml of the solution is taken out and is titrated to a neutral endpoint with 0.10 m NaOH. The titrated portion is then mixed with the remaining untitrated portion and the pH of the mixture is measured.

Mass of acid weighed out (grams) 0.755
Volume of NaOH required to reach endpoint: (ml) 18.8
pH of the mixture (half neutralized solution) 3.51
1. What is the pKa of the acid?

Answer 1

pKa = 3.51

Step-by-step explanation:

The titration of acid solution with NaOH can be illustrated as:

`AH + NaOH \to NaA + H_2O`

Given that:

Volume of acid solution
`(V_1) = 25 \ mL`

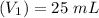
Volume of NaOH
`(V_2) = 18.8 \ mL`

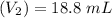
Molarity of acid solution
`(M_1) = ???`

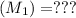
Molarity of NaOH
`(M_2) = 0.10 \ M`

For Neutralization reaction:

`M_1V_1 = M_2V_2`

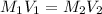
Making
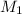`M_1` the subject of the formula; we have:

`M_1 = (M_2V_2)/(V_1)`

`M_1 = (0.10*18.8)/(25)`

`M_1 =0.0752 \ M`

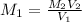
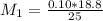
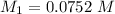
However; since the number of moles of NaA formed is equal to the number of moles of NaOH used : Then :

`M_2V_2 = 0.10 *18.8 = 1.88 \ mm`

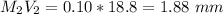
Total Volume after titration = ( 25 + 18.8 ) m

= 43.8 mL

Molarity of salt (NaA ) solution =
`(number \ of \ moles)/(Volume \ (mL))`

=
`(1.88)/(43.8)`

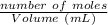
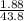
= 0.0429 M

After mixing the two solution ; the volume of half neutralize solution is = 25 mL + 43.8 mL

= 68.8 mL

Molarity of NaA before mixing
`M_1 = 0.0429 \ M`

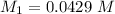
Volume
`(V_1) = 43.8 \ mL`

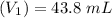
Molarity of NaA after mixing
`M_2 = ???`

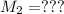
Volume
`(V_2 ) = 68.8 \ mL`

∴

`M_2 = (M_1*V_1)/(V_2) \\ \\ M_2 = (0.0429*43.1)/(68.8) \\ \\ M_2 = 0.0273 \ M`

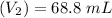
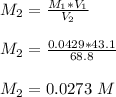
Molarity of acid before mixing = 0.0725 M

Volume = 25 mL

Molarity of acid after mixing =
`(0.0752*25)/(68.8)`

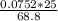
= 0.0273 M

Since this is a buffer solution ; then using Henderson Hasselbalch Equation

`pH = pKa + log ([salt])/([acid])`

`3.51= pKa + log ([0.0273])/([0.0273]) \\ \\ 3.51= pKa + log \ 1 \\ \\ 3.51= pKa + 0 \\ \\ pKa = 3.51`