Answer:
40 rad/s
Step-by-step explanation:
The moment of inertia around the disk pulley is

A force of 50N around the pulley of radius 0.2m would generate a torque of T = 50*0.2 = 10 Nm. According to Newton's 2nd law this torque would make an angular acceleration of:
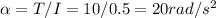
The angular speed after ∆ t=2 when it starts from rest at that constant angular acceleration is
