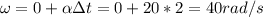Question

A pulley, consists of a disk of radius R=0.2 m and mass M= 25 kg is mounted on a nearly frictionless axle. A string is wrapped lightly around the pulley, and you pull on the string with a constant force, F = 50 N. If the pulley starts from rest, what is the angular speed at a time ∆ t=2 s later? Assume that the string does not slip on the pulley. Note: Moment of inertia of a disk about an axis through its center of mass is Idisk = (1/2) MR2

Answer 1

40 rad/s

Step-by-step explanation:

The moment of inertia around the disk pulley is

`I = MR^2/2 = 25*0.2^2/2 = 0.5 kgm^2`

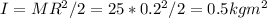
A force of 50N around the pulley of radius 0.2m would generate a torque of T = 50*0.2 = 10 Nm. According to Newton's 2nd law this torque would make an angular acceleration of:

`\alpha = T/I = 10 / 0.5 = 20 rad/s^2`

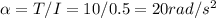
The angular speed after ∆ t=2 when it starts from rest at that constant angular acceleration is

`\omega = 0 + \alpha \Delta t = 0 + 20*2 = 40 rad/s`