Question

A block of plastic in the shape of a rectangular solid that has height 8.00 cm and area A for its top and bottom surfaces is floating in water. You place coins on the top surface of the block (at the center, so the top surface of the block remains horizontal). By measuring the height of the block above the surface of the water, you can determine the height h below the surface. You measure h for various values of the total mass m of the coins that you have placed on the block. You plot h versus m and find that your data lie close to a straight line that has slope 0.0890 m/kg and y-intercept 0.0312 m. Part A What is the mass of the block?

Answer 1

0.35 kg

Step-by-step explanation:

8 cm = 0.08 m

For the block to stay balance, the buoyancy force must be the same as gravity that pulls it down.

Let mass of the block be M, then the gravity would be Mg

Let water density be
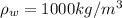`\rho_w = 1000 kg/m^3`, the buoyancy force would be the weight of water that is displaced by the submerged block.

For example, when there is no coin, block is
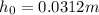`h_0 = 0.0312m` submerged. The weight of water displaced must be

`W_0 = Ah_0\rho_wg = 0.0312A1000g = 31.2Ag`

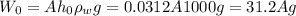
Which is also the weight of block, of Mg

Therefore M = 31.2A. (1)

As coins are stacked on top of block, h increase, so as weight of water displaced and total weight of block and coins. Now let m be the total weight of coins. The gravity of block and weight must be (M+m)g. And the weight of water displaced is:

`W = Ah\rho g = (M + m)g`

`h = (M)/(A\rho) + (m)/(A\rho)`

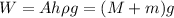
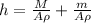
Since the linear plot of h vs m has a slope of 0.089 m/kg, we can interpret it as

`(1)/(A\rho) = 0.089`

`A = (1)/(0.089\rho) = (1)/(89) = 0.011 m^2`

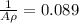
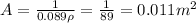
So from the eq. (1) we can solve for M = 31.2A = 0.35 kg