Answer:
0.35 kg
Step-by-step explanation:
8 cm = 0.08 m
For the block to stay balance, the buoyancy force must be the same as gravity that pulls it down.
Let mass of the block be M, then the gravity would be Mg
Let water density be
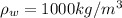 , the buoyancy force would be the weight of water that is displaced by the submerged block.
, the buoyancy force would be the weight of water that is displaced by the submerged block.
For example, when there is no coin, block is
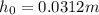 submerged. The weight of water displaced must be
submerged. The weight of water displaced must be
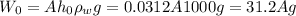
Which is also the weight of block, of Mg
Therefore M = 31.2A. (1)
As coins are stacked on top of block, h increase, so as weight of water displaced and total weight of block and coins. Now let m be the total weight of coins. The gravity of block and weight must be (M+m)g. And the weight of water displaced is:
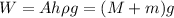
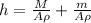
Since the linear plot of h vs m has a slope of 0.089 m/kg, we can interpret it as
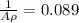
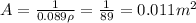
So from the eq. (1) we can solve for M = 31.2A = 0.35 kg