Question

HELPPPPP: DUE IN AN HOUR
Find the volume of the composite solid. Round to the nearest tenth.

Answer 1

1. 1206.3 ft cubed

2. 121.9 units cubed

3. 120.1 in cubed

Explanation:

1. This solid is made up of a cone and a cylinder. The volume of a cone is denoted by:
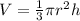`V=(1)/(3) \pi r^2h`, where r is the radius and h is the height. Here, the diameter is 16, which means the radius is r = 16/2 = 8, and the height is h = 6. Plug these in:

`V=(1)/(3) \pi r^2h`

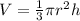
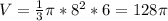`V=(1)/(3) \pi *8^2*6=128\pi` ≈ 402.1

The volume of a cylinder is denoted by:
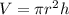`V=\pi r^2h`, where r is the radius and h is the height. Here, again, the radius is r = 16/2 = 8, but the height is h = 4. Plug these in:

`V=\pi r^2h`

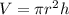
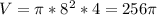`V=\pi *8^2*4=256\pi` ≈ 804.2

Adding these two values together, we get:

402.1 + 804.2 = 1206.3 ft cubed.

2. In order to find the volume of this, we need to subtract the volume of the hemisphere from the volume of the cylinder. We know that the radius of the cylinder is r = 7/2 and the height is 5.5, so:

`V=\pi r^2h`

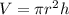
`V=\pi (7/2)^2*5.5=67.375\pi` ≈ 211.7

The volume of a hemisphere is denoted by:
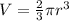`V=(2)/(3) \pi r^3`, where r is the radius. Here, the radius is r = 7/2, so plug this in:

`V=(2)/(3) \pi r^3`

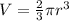
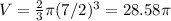`V=(2)/(3) \pi (7/2)^3=28.58\pi` ≈ 89.8

Subtract this from the first value:

211.7 - 89.8 = 121.9 units cubed

3. This solid is made up of a sphere, a cylinder, and a rectangular prism. The volume of a sphere is:
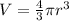`V=(4)/(3) \pi r^3`, where r is the radius. Here, r = 5/2, so:

`V=(4)/(3) \pi r^3`

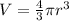
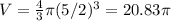`V=(4)/(3) \pi (5/2)^3=20.83\pi` ≈ 65.4

The radius of the cylinder is r = 1/2 and the height is h = 6, so plug these in:

`V=\pi r^2h`

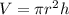
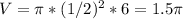`V=\pi *(1/2)^2*6=1.5\pi` ≈ 4.7

The volume of a rectangular prism is denoted by:
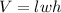`V=lwh`, where l is the length, w is the width, and h is the height. Here, l = 5, w = 5, and h = 2. Plug these in:

`V=lwh`

`V=5*5*2=50`

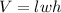
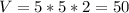
Add all three values together:

65.4 + 4.7 + 50 = 120.1 in cubed

Hope this helps!