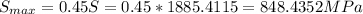Answer:
Kc = 1.0844
Smax = 848.4352 MPa
Step-by-step explanation:
Given data:
d = diameter = 3 mm
D = outside diameter = 35 mm
N = coils = 16
Spring fully compressed
Question: What is the curvature correction factors, Kc = ? and the maximum shear, Smax = ?
First, Dm needs to be calculated:
Dm = D - d = 35 - 3 = 32 mm
The spring index:
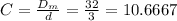
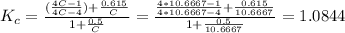
Properties at a diameter of 3 mm:
Area = A = 2211 MPa mm^m
m = 0.145
The shear stress:
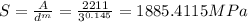
According the distortion theory, the maximum shear: