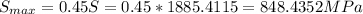Question

A helical compression spring is wound using 3 mm diameter music wire. The spring has an outside diameter of 35 mm with plain ground ends and 16 coils If the spring does not yield when the spring is fully compressed, what is curvature correction factors Kc and the maximum shear that will be in the spring?

Answer 1

Kc = 1.0844

Smax = 848.4352 MPa

Step-by-step explanation:

Given data:

d = diameter = 3 mm

D = outside diameter = 35 mm

N = coils = 16

Spring fully compressed

Question: What is the curvature correction factors, Kc = ? and the maximum shear, Smax = ?

First, Dm needs to be calculated:

Dm = D - d = 35 - 3 = 32 mm

The spring index:

`C=(D_(m) )/(d) =(32)/(3) =10.6667`

`K_(c) =(((4C-1)/(4C-4))+(0.615)/(C) )/(1+(0.5)/(C) ) =((4*10.6667-1)/(4*10.6667-4) +(0.615)/(10.6667) )/(1+(0.5)/(10.6667) ) =1.0844`

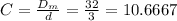
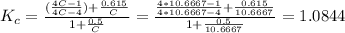
Properties at a diameter of 3 mm:

Area = A = 2211 MPa mm^m

m = 0.145

The shear stress:

`S=(A)/(d^(m) ) =(2211)/(3^(0.145) ) =1885.4115MPa`

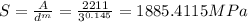
According the distortion theory, the maximum shear:

`S_(max) =0.45S=0.45*1885.4115=848.4352MPa`

Answer 2

Kc = 1.0844

Maximum shear = 848.43 Mpa

Step-by-step explanation:

Find attached of the calculations