Answer:
i ) Radhika
ii ) Supriya
iii) Hema
Step-by-step explanation:
Solution:-
- Radhika ,Supriya and Hema were asked to find the mass of a metal piece independently one by one using the same balance and same weight box.
- Each student was asked to take three observations. The students reported their result as shown in the following table:
1st 2nd 3rd 4th
Radikha 1.325 1.326 1.325 1.325
Supriya 1.310 1.311 1.321 1.314
Hema 1.31 1.30 1.31 1.31
- The actual mass, u = 1.325 g , permitted uncertainty = 0.001 g
- We will use the data given and determine true important parameters for each student. These are mean value (X,Y or Z) and standard deviation ( Sx,Sy or Sz ). There are n = 4 data points for each student.
Radikha:-
Sample Mean ( X )
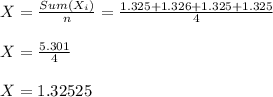
Standard deviation ( Sx )
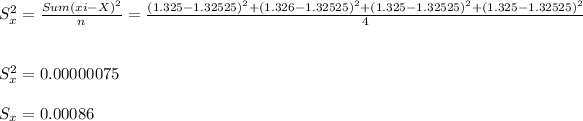
Supriya:-
Sample Mean ( Y )
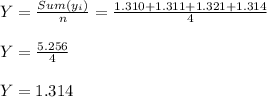
Standard deviation ( Sy )
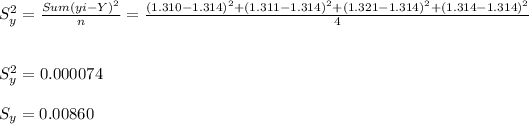
Hema:-
Sample Mean ( Z )
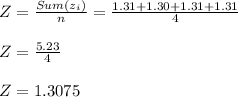
Standard deviation ( Sz )

- Now, we will compare the sample mean and sample standard deviation for each student with the actual mass of metal piece and the permitted uncertainty.
Radhika:- X = 1.32525 , Sx = 0.00086 grams.
- The actual mass and sample average mass are close to 4th decimal place making it the most accurate measurement out of all.
- The standard deviation ( Sx ) is the uncertainty in the measurements taken = 0.00086 is well within the permitted allowance of 0.001 grams. Hence, the most precise and accurate measurements were taken by Radhika.
Supriya:- Y = 1.314 , Sy = 0.0086 grams.
- The actual mass and sample average mass are off by:
Error = ( 1.325 - 1.314 )*100 / 1.325
= 0.83 %
- Not as accurate but,
- The standard deviation ( Sy ) is the uncertainty in the measurements taken = 0.0086 is well good around the permitted allowance of 0.001 grams. Hence, her measurement were not that accurate but had good precision.
Hema:- Z = 1.3075 , Sz = 0.05068 grams.
- The actual mass and sample average mass are off by:
Error = ( 1.325 - 1.3075 )*100 / 1.325
= 1.32 %
- Least accurate and,
- The standard deviation ( Sy ) is the uncertainty in the measurements taken = 0.05068 is poor for the permitted allowance of 0.001 grams. Hence, her measurement were neither accurate nor had good precision .