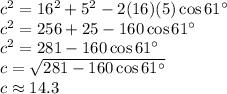Answer:
AB ≈ 14.3
Explanation:
We're given two sides (BC and CA) and an angle (C) between them; the law of cosines is a good tool for calculating the third side of the triangle here. To remind you, the law of cosines tells us the relationship between the sides of a triangle with side lengths a, b, and c:
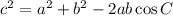
Where C is the angle between sides a and b. c is typically the side we're trying to find, so on our triangle, we have
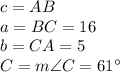
Substituting these values into the law of cosines: