Question

A new car is purchased for 15100 dollars. The value of the car depreciates at 13% per year. To the nearest tenth of a year, how long will it be until the value of the car is 1900 dollars?

Answer 1

14.9 thx me later

Explanation:

Answer 2

The price of car will be $1,900 after 14.9 years.

Explanation:

Formula of depreciate:

`A=P(1-r)^n`

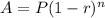
A= The price of the car after n years.

P= The initial price of the car

r= rate of depreciate

n=time in years.

Given that,

A new car is purchased for $ 15,100.

The value of car depreciates at 13% per year.

Here P=$15,100, A=$1,900, r=13%=0.13, n=?

`A=P(1-r)^n`

`\Rightarrow 1,900=15,100(1-0.13)^n`

`\Rightarrow (1,900)/(15,100)=(0.87)^n`

`\Rightarrow (0.87)^n= (1,900)/(15,100)`

`\Rightarrow (0.87)^n= (19)/(151)`

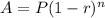
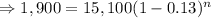
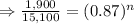
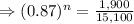
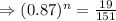
Tanking ln function both sides

`\Rightarrow ln (0.87)^n= ln|(19)/(151)|`

`\Rightarrow nln (0.87)= ln|(19)/(151)|`

`\Rightarrow n= (ln|(19)/(151)|)/(ln (0.87))`

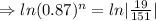
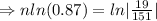
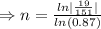
⇒n ≈14.9

The price of car will be $1,900 after 14.9 years.