Answer:
The price of car will be $1,900 after 14.9 years.
Explanation:
Formula of depreciate:
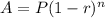
A= The price of the car after n years.
P= The initial price of the car
r= rate of depreciate
n=time in years.
Given that,
A new car is purchased for $ 15,100.
The value of car depreciates at 13% per year.
Here P=$15,100, A=$1,900, r=13%=0.13, n=?
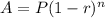
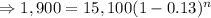


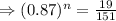
Tanking ln function both sides
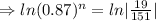
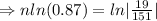

⇒n ≈14.9
The price of car will be $1,900 after 14.9 years.