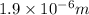Question

Consider a Hydrogen atom in the 3rd excited state (n = 4). The maximum wavelength of light that can be emitted is

9.7 x 10^-8 m
1.9 x 10^-6 m
1.03 x 10^-7 m
2.5 x 10^-5 m

Answer 1

Answer: The maximum wavelength of light that can be emitted is
`1.9* 10^(-6)m`

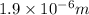
Step-by-step explanation:

`E=(hc)/(\lambda)`

`\lambda` = Wavelength of radiation

E= energy

For wavelength to be maximum, energy would be minimum, i.e the electron will jump from n=4 level to n =3

Using Rydberg's Equation:

`(1)/(\lambda)=R_H\left((1)/(n_i^2)-(1)/(n_f^2) \right )* Z^2`

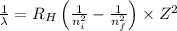
Where,

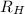`R_H` = Rydberg's Constant =
`1.097* 10^7m^(-1)`

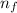`n_f` = Higher energy level = 3

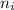`n_i` = Lower energy level = 4

Z= atomic number = 1 (for hydrogen)

`(1)/(\lambda)=1.097* 10^7\left((1)/(3^2)-(1)/(4^2) \right )* 1^2`

`(1)/(\lambda)=0.053* 10^7`

`\lambda=1.9* 10^(-6)m`

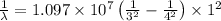
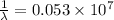
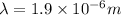
Thus the maximum wavelength of light that can be emitted is
`1.9* 10^(-6)m`