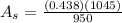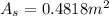Question

Cold water (cp = 4180 J/kg·K) leading to a shower enters a thin-walled double-pipe counterflow heat exchanger at 15°C at a rate of 0.25 kg/s and is heated to 45°C by hot water (cp = 4190 J/kg·K) that enters at 100°C at a rate of 3 kg/s. If the overall heat transfer coefficient is 950 W/m2·K, determine the rate of heat transfer and the heat transfer surface area of the heat exchanger using the ε–NTU method. Answers: 31.35 kW, 0.482 m2

Answer 1

The rate of heat transfer is
`H = 31.35\ kW`

The heat transfer surface area is
`A_s = 0.4818 m^2`

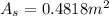
Step-by-step explanation:

From the question we are told that

The specific heat of water is
`cp = 4180 \ J/kg \cdot K`

The temperature of cold water is
`T_c = 15^o C`

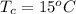
The rate of cold the flow is
`\r m = 0.25 kg/s`

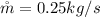
The temperature of the heated water
`T_h = 45 ^oC`

The specific heat of hot water is
`c_p__(H)} = 4190 J/kg \cdot K`

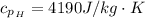
The temperature of the hot water is
`T_H = 100^oC`

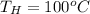
The rate of hot the flow is
`\r m_H = 3 kg/s`

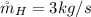
The heat transfer coefficient is
`U = 950 W/m^2 \cdot K,`

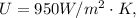
From the
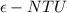`\epsilon -NTU` method we have that

`C_h = \r m_H c_p__(H)}`

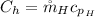
Where
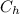`C_h` is the heat capacity rate of hot water

Substituting the value

`C_h = 3 * (4190)`

`= 12,5700\ W/^oC`

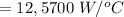
Also

`C_c = \r m c_p`

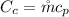
Where
`C_c` is the heat capacity rate of cold water

`C_c = 0.25 * 4180`

`= 1045 \ W / ^oC`

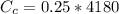
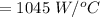
The maximum heat capacity
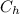`C_h` and the minimum heat capacity is
`C_c`

The maximum heat transfer is

`H_(max) = C_c (T_H - T_c)`

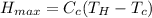
Substituting values

`H_(max) = (1045)(100- 15)`

`= 88,825\ W`

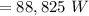
The actual heat transfer is mathematically evaluated as

`H = C_c (T_h - T_c)`

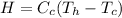
Substituting values

`H = 1045 (45 - 15 )`

`H = 31350 \ W`

`H = 31.35\ kW`

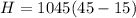
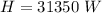
The effectiveness of the heat exchanger is mathematically evaluated as

`\epsilon = (H)/(H_(max))`

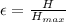
Substituting values

`\epsilon = (31350)/(88,825)`

`= 0.35`

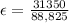
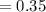
The NTU of the heat exchanger is mathematically represented as

`NTU = (1)/(C-1) ln [(\epsilon - 1)/(\epsilon C -1) ]`

Where C is the ratio of the minimum to the maximum heat capacity which is mathematically represented as

`C = (C_c)/(C_h)`

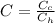
Substituting values

`C = (1045)/(12,570)`

`= 0.083`

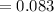
Substituting values in to the equation for NTU

`NTU = (1)/(0.083 -1) ln[(0.35 - 1)/(0.35 * (0.083 - 1)) ]`

`= 0.438`

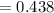
Generally the heat transfer surface area can be mathematically represented as

`A_s = (NTU C_c)/(U)`

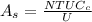
Substituting values

`A_s = ((0.438) (1045))/(950)`

`A_s = 0.4818 m^2`