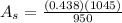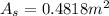Answer:
The rate of heat transfer is
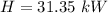
The heat transfer surface area is
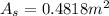
Step-by-step explanation:
From the question we are told that
The specific heat of water is
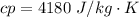
The temperature of cold water is
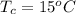
The rate of cold the flow is
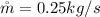
The temperature of the heated water
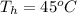
The specific heat of hot water is
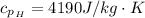
The temperature of the hot water is
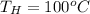
The rate of hot the flow is
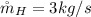
The heat transfer coefficient is
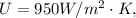
From the
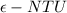 method we have that
method we have that
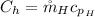
Where
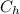 is the heat capacity rate of hot water
is the heat capacity rate of hot water
Substituting the value
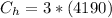
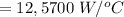
Also
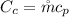
Where
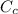 is the heat capacity rate of cold water
is the heat capacity rate of cold water
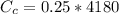
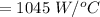
The maximum heat capacity
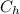 and the minimum heat capacity is
and the minimum heat capacity is
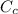
The maximum heat transfer is
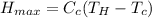
Substituting values
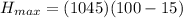
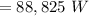
The actual heat transfer is mathematically evaluated as
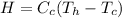
Substituting values
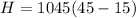
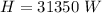
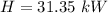
The effectiveness of the heat exchanger is mathematically evaluated as
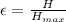
Substituting values
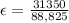
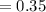
The NTU of the heat exchanger is mathematically represented as
![NTU = (1)/(C-1) ln [(\epsilon - 1)/(\epsilon C -1) ]](https://img.qammunity.org/2021/formulas/engineering/college/pl7mrhowkj9nx9kre6mhyahtv14stixr59.png)
Where C is the ratio of the minimum to the maximum heat capacity which is mathematically represented as
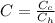
Substituting values
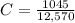
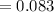
Substituting values in to the equation for NTU
![NTU = (1)/(0.083 -1) ln[(0.35 - 1)/(0.35 * (0.083 - 1)) ]](https://img.qammunity.org/2021/formulas/engineering/college/57iqikti9uwq88q07vy4p95xyb3d85ow2n.png)
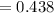
Generally the heat transfer surface area can be mathematically represented as
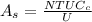
Substituting values