Answer:
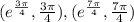 .
.
Explanation:
REcall that given a parametric curve x(t),y(t), the tangent's line slope is given by
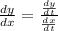
To find where the tangent line is horizontal, we must find where the slope is 0. That is, to find the values of t for which
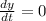 and
and
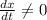 at the same time.
at the same time.
Consider the polar curve
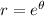 . If we use the polar coordinates, we have that
. If we use the polar coordinates, we have that
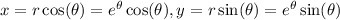 , which gives us a parametric curve with parameter
, which gives us a parametric curve with parameter
 . So, let us use the above to find the desired points.
. So, let us use the above to find the desired points.
We have that
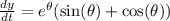
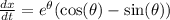
Recall that the function
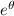 is never 0, so, for us to have the derivative of y to be 0, we must have that
is never 0, so, for us to have the derivative of y to be 0, we must have that
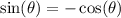 . Note that if this happens, the derivative of x is different from 0. So, we must solve the following equation in the interval
. Note that if this happens, the derivative of x is different from 0. So, we must solve the following equation in the interval
![\theta \in [0,2\pi]](https://img.qammunity.org/2021/formulas/mathematics/college/ueqp2sy0cl5isegiftsa0hj2756hy1f73l.png) .
.
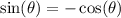 , which is equivalent to
, which is equivalent to
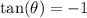 . Which gives us
. Which gives us
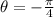 . This solution is out of our desired interval, then , using the fact that tangent is a periodic function with period pi, we can find the solutions in the desired interval by adding multiples of pi. Thus, the desired solutions are
. This solution is out of our desired interval, then , using the fact that tangent is a periodic function with period pi, we can find the solutions in the desired interval by adding multiples of pi. Thus, the desired solutions are
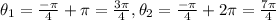
Note that
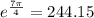 and
and
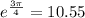 ,so both solutions are inside the restriction.
,so both solutions are inside the restriction.