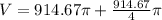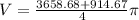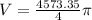Question

Use spherical coordinates to find the volume of the region bounded by the sphere rhoequals28 cosine phi and the hemisphere rhoequals14​, zgreater than or equals0. An x y z coordinate system has an x-axis with a tick mark at 14, a y-axis with a tick mark at 14, and a vertical positive z-axis with an unlabeled tick mark. A hemisphere has a circular base in the x y plane with center at the origin and radius 14, and its point farthest from the origin is on the positive z-axis at the unlabeled tick mark. A sphere has its center on the positive z-axis at the unlabeled tick mark and its lowest point at the origin. In the plane parallel to the x y axis at the unlabeled positive z-axis tick mark, the sphere's has its point with the greatest x-coordinate, at 14, and its point with the greatest y-coordinate, at 14. x y z 14 14 The volume of the region bounded by the sphere and the hemisphere is nothing. ​(Type an exact​ answer, using pi as​ needed.)

Answer 1

the volume of the region bounded by the sphere
`V=(4573.35)/(4) \pi`

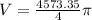
Explanation:

Let assume the region is A;

Given that; the region A is bounded by the sphere
`\rho = 28 cos \phi` and the hemisphere
`\rho = 14, z \geq 0`

The intersection of two curves is given by :

`28 cos \phi = 14 \\ \\ cos \phi = (1)/(2) \\ \\ \phi = (\pi)/(3)`

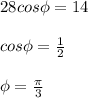
Using spherical coordinates to find the volume of the region bounded by the sphere; we have:

`\rho ^2 = x^2 +y^2 + z^2 \\ \\ x = \rho \ sin \ \phi \ cos \ \theta \\ \\ y = \rho \ sin \ \phi \ sin \ \theta \\ \\ z = \rho \ cos \ \phi`

`dxdydz = \rho^2 sin \phi \ d \rho \ d\phi \ d\theta`

`V = \int\limits^(2\pi)_0 \int\limits^{(\pi)/(3)}_0 \int\limits^(14)_0 \ \rho^2 sin \phi d \rho d \phi d \theta + \int\limits^(2\pi)_0 \int\limits^{(\pi)/(2)}_{(\pi)/(3)} \int\limits^(28 cos \phi)_0 \ \rho^2 sin \phi d \rho d \phi d \theta`

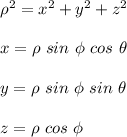
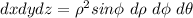
`V = \int\limits^(2\pi)_0 \int\limits^{(\pi)/(3)}_0 [(\rho^3)/(3)]^(14)__0}} \ sin \phi d \phi d \theta + \int\limits^(2\pi)_0 \int\limits^{(\pi)/(2)}_{(\pi)/(3)} [(\rho^3)/(3)]^(28 cos \phi)__0}} \ sin \phi d \phi d \theta`

`V = 914.67 \ \int\limits^(2\pi)_0 \int\limits^{(\pi)/(3)}_0 \ sin \phi d \phi d \theta + 7317.33 \ \int\limits^(2\pi)_0 \int\limits^{(\pi)/(2)}_{(\pi)/(3)} cos^3 \phi} \ sin \phi d \phi d \theta`

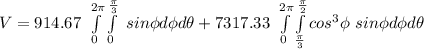
`V = 914.67[-cos \phi]^{(\pi)/(3)}}__0}}}[\theta]^(2\pi)__0}} + 7317.33[- (cos^4 \phi)/(4)]^{(\pi)/(2)}__{(\pi)/(3)}} [\theta]^(2 \pi)_o`

`V = 914.67[-(1)/(2)+1](2 \pi) + 7317.33[ (1)/(64)](2 \pi)`

`V = 914.67 \pi + \frac {914.67 }{4} \pi`

`V =(3658.68+914.67)/(4) \pi`

`V =(4573.35)/(4) \pi`