Question

How do you find the value of c that satisfy the equation:

f(b)- f(a)/b-a = f'(c)

in the conclusion of the mean value theorem for the function
f(x)= 4x^2 + 4x -3 on the interval [-1,0]?

Answer 1

The value of c = -0.5∈ (-1,0)

Explanation:

Step(i):-

Given function f(x) = 4x² +4x -3 on the interval [-1 ,0]

Mean Value theorem

Let 'f' be continuous on [a ,b] and differentiable on (a ,b). The there exists a Point 'c' in (a ,b) such that

`f^(l) (c) = (f(b) -f(a))/(b-a)`

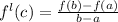
Step(ii):-

Given f(x) = 4x² +4x -3 …(i)

Differentiating equation (i) with respective to 'x'

f¹(x) = 4(2x) +4(1) = 8x+4

Step(iii):-

By using mean value theorem

`f^(l) (c) = (f(0) -f(-1))/(0-(-1))`

`8c+4 = (-3-(4(-1)^2+4(-1)-3))/(0-(-1))`

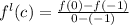
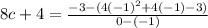
8c+4 = -3-(-3)

8c+4 = 0

8c = -4

`c = (-4)/(8) = (-1)/(2) = -0.5`

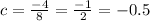
c ∈ (-1,0)

Conclusion:-

The value of c = -0.5∈ (-1,0)