Answer:
The value of c = -0.5∈ (-1,0)
Explanation:
Step(i):-
Given function f(x) = 4x² +4x -3 on the interval [-1 ,0]
Mean Value theorem
Let 'f' be continuous on [a ,b] and differentiable on (a ,b). The there exists a Point 'c' in (a ,b) such that
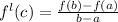
Step(ii):-
Given f(x) = 4x² +4x -3 …(i)
Differentiating equation (i) with respective to 'x'
f¹(x) = 4(2x) +4(1) = 8x+4
Step(iii):-
By using mean value theorem
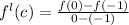
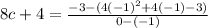
8c+4 = -3-(-3)
8c+4 = 0
8c = -4
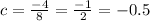
c ∈ (-1,0)
Conclusion:-
The value of c = -0.5∈ (-1,0)