Answer:
Assuming 312 operating days, the number of days between orders will be
= 312 days / 26 orders
= 12 days
Step-by-step explanation:
EOQ =
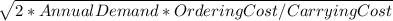
Annual demand = weekly usage * assumed number of weeks in a year
= 4 pounds * 52 weeks
= 208 pounds
Carrying cost for the year = $1 * 52 weeks = $52
Ordering cost = $8
∴ EOQ =
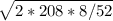
=
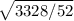
=
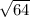
Economic Order Quantity = 8 pounds
Since EOQ is 8 pounds and annual demand is 208 pounds
∴ number of orders in the year = 208/8
= 26 orders