Answer:
1.52 m
Step-by-step explanation:
We are given that
Maximum force=F=679 N
Mass of rock ,m=385 kg
Distance,d=0.233 m
We have to find the minimum total length L of the rod required to move the rock.
Torque on rock=
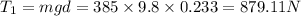
Where
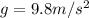
Torque on man=
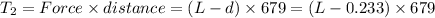
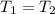
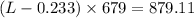
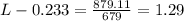
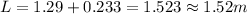
Hence, the minimum total length of rod=1.52 m