Question

Question: An airport deli sells turkey, ham, and roast beef sandwiches. A customer can choose between turkey,

ham, and roast beef, if it does or does not have cheese on it, and it may or may not have mayonnaise
on it. If Ginger randomly selects one meat, cheese or no cheese, and mayonnaise or no mayonnaise,
and she is equally likely to select each sandwich ingredient, what is the probability Ginger selected a
roast beef sandwich with cheese and without mayonnaise?

Answer 1

`\displaystyle (1)/(12)`.

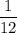Step-by-step explanation:

Ginger selects the ingredients randomly. Therefore, the choices she makes would be independent. In other words, her choice of cheese (and mayonnaise) won't depend on what she chose for meat. Therefore:

`\begin{aligned}& P(\text{(roast beef) and (cheese) and (no mayonnaise)}) \\ &= P(\text{roast beef})\cdot P(\text{cheese}) \cdot P(\text{no mayonnaise})\end{aligned}`.

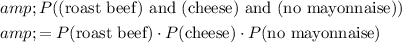It is worth noting that this equality would not be valid if the choices are not independent. For example, if Ginger is more likely to choose mayonnaise after choosing cheese, then
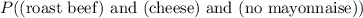`P(\text{(roast beef) and (cheese) and (no mayonnaise)})` and
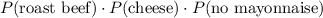`P(\text{roast beef})\cdot P(\text{cheese}) \cdot P(\text{no mayonnaise})` would likely be different.

What is the probabilities that Ginger would select roast beef for the sandwich? The question states that Ginger is "equally likely" to select each of turkey, ham, and roast beef. In other words:

`P(\text{roast beef})= P(\text{turkey}) = P(\text{ham})`.

At the same time, Ginger has to choose exactly one of these options. She can't choose no meat of more than one options at a time. Therefore:

`P(\text{roast beef})+ P(\text{turkey}) + P(\text{ham}) = 1`.

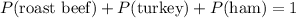Combine these two equations to conclude that:

• 
  `\displaystyle P(\text{roast beef}) = (1)/(3)`.

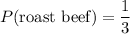Similarly, Ginger has to choose between cheese or no cheese, and mayonnaise or no mayonnaise. Therefore:

• 
  `\displaystyle P(\text{cheese}) = (1)/(2)`.
• 
  `\displaystyle P(\text{mayonnaise}) = (1)/(2)`.

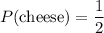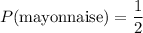Back to the probability for roast beef, cheese, and no mayonnaise:

`\begin{aligned}& P(\text{(roast beef) and (cheese) and (no mayonnaise)}) \\ &= P(\text{roast beef})\cdot P(\text{cheese}) \cdot P(\text{no mayonnaise}) \\ &= (1)/(3) * (1)/(2) * (1)/(2) \\ &= (1)/(12)\end{aligned}`.