Question

Researchers are studying two populations of sea turtles. In population D, 30 percent of the turtles have a shell length greater than 2 feet. In population E, 20 percent of the turtles have a shell length greater than 2 feet. From a random sample of 40 turtles selected from D, 15 had a shell length greater than 2 feet. From a random sample of 60 turtles selected from E, 11 had a shell length greater than 2 feet. Let pˆD represent the sample proportion for D, and let pˆE represent the sample proportion for E.

Question 2
(b) What are the mean and standard deviation of the sampling distribution of the difference in sample proportions pˆD−pˆE ? Show your work and label each value.

(c) Can it be assumed that the sampling distribution of the difference of the sample proportions pˆD−pˆE is approximately normal? Justify your answer.

(d) Consider your answer in part (a). What is the probability that pˆD−pˆE is greater than the value found in part (a)? Show your work

Answer 1

The mean of the sampling distribution is approximately 0.192 and the standard deviation is approximately 0.080.

Step-by-step explanation:

To find the mean and standard deviation of the sampling distribution of the difference in sample proportions (pˆD - pˆE), we can use the formulas:

Mean (μ) = pD - pE

Standard Deviation (σ) = sqrt(( pD*(1 - pD)/nD ) + ( pE*(1 - pE)/nE ))

Given the information provided, pD = 15/40 = 0.375, pE = 11/60 ≈ 0.183, nD = 40, and nE = 60. Plugging these values into the formulas, we get:

Mean = 0.375 - 0.183 ≈ 0.192

Standard Deviation ≈ sqrt((0.375*(1 - 0.375)/40) + (0.183*(1 - 0.183)/60)) ≈ 0.080.

Answer 2

a. 0.1917

b. 0.0914

d. 0.1580

Step-by-step explanation:

(a)

`P^D = (15)/(40) = 0.375`

`P^E = (11)/(60) =0.8133`

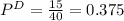
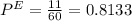
Mean,
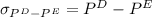`\sigma_(P^D-P^E) = P^D-P^E` = 0.375 -0.1833 = 0.1917

(b) sample prop ? Show your work and label each value.

Mean, = = 0.1917

Standard deviation =
`\sqrt{(P^D(1-P^D))/(N_D) +(P^E(1-P^E))/(N_E) }`

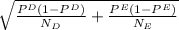
Standard deviation =
`\sqrt{(0.375(1-0.375))/(40) +(0.1833(1 - 0.1833))/(60) }`

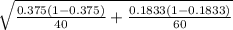
Standard deviation = 0.0914

(c)

Normality condition:

np ≥ 10 and n(1-p) ≥ 10

Both the samples satisfy the normality condition.

(d)

The probability is obtained by calculating the z score,

`z = ((P^D-P^E)-(P^d-P^e))/(\sigma_(P^D - P^E))`

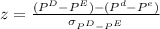
`z = (0.1917-0.1)/(0.0914)` = 1.0029

P(z > 1.0029) = 1 - P(z ≤ 1.0029)

The probability is obtained from the z distribution table,

P(Z > 1.0029) = 1 - 0.8420 = 0.1580