Answer:
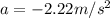
Step-by-step explanation:
the information we have is:
initial velocity:
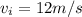
final velocity:
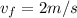
and the time:
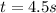
We need to find the acceleration of the car.
For this we use formula to calculate the acceleration given the information we were given:
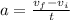
acceleration is equal to the difference between the final velocity and the initial velocity divided by time.
We substitute all the known values:
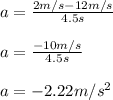
the acceleration is
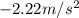
the result is negative because the car is slowing down.