Answer:
3. The model for a substance of 400 mg with a half-life of 84 days is:
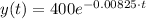
4. 160 mg.
5. It will take 7 years for Ahmed's account to accumulate $500.
Explanation:
3. We can write a model for the substance with exponential decay as:
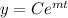
We know that at time t=0, the mass is 400 mg.
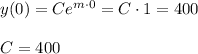
We also know that the half-life is 84 days, so at t=84 days, the mass will be 400/2=200 mg.
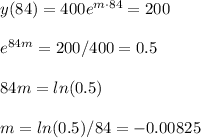
The model for a substance of 400 mg with a half-life of 84 days is:
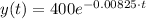
4. After 110 days the substance will have a mass of y=160 mg.
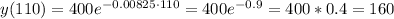
5. The amount that Ahmed's will acumulate in function of the years (n) can be written as:
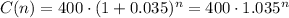
We can calculate how many years it will take for the Amhed's account to acumulate $500 as:
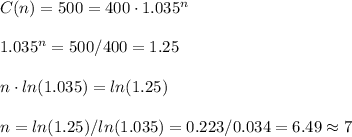
It will take 7 years for Ahmed's account to accumulate $500.