Question

3. Write a function that models 400 mg of a substance that has a half-life of 84 days.

4. Using the same data in #3, how much of the substance will be left after 110 days?

5. Ahmed invests $400 into a back account that pays 3.5% interest annually. How long will
it take Ahmed's account to accumulate $500?

Answer 1

3. The model for a substance of 400 mg with a half-life of 84 days is:

`y(t)=400e^(-0.00825\cdot t)`

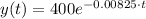
4. 160 mg.

5. It will take 7 years for Ahmed's account to accumulate $500.

Explanation:

3. We can write a model for the substance with exponential decay as:

`y=Ce^(mt)`

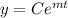
We know that at time t=0, the mass is 400 mg.

`y(0)=Ce^(m\cdot0)=C\cdot 1=400\\\\C=400`

We also know that the half-life is 84 days, so at t=84 days, the mass will be 400/2=200 mg.

`y(84)=400e^(m\cdot84)=200\\\\e^(84m)=200/400=0.5\\\\84m=ln(0.5)\\\\m=ln(0.5)/84=-0.00825`

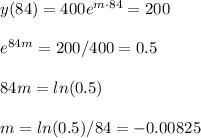
The model for a substance of 400 mg with a half-life of 84 days is:

`y(t)=400e^(-0.00825\cdot t)`

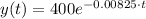
4. After 110 days the substance will have a mass of y=160 mg.

`y(110)=400e^(-0.00825\cdot 110)=400e^(-0.9)=400*0.4=160`

5. The amount that Ahmed's will acumulate in function of the years (n) can be written as:

`C(n)=400\cdot(1+0.035)^n=400\cdot1.035^n`

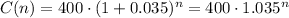
We can calculate how many years it will take for the Amhed's account to acumulate $500 as:

`C(n)=500=400\cdot 1.035^n\\\\1.035^n=500/400=1.25\\\\n\cdot ln(1.035)=ln(1.25)\\\\n=ln(1.25)/ln(1.035)=0.223/0.034=6.49\approx7`

It will take 7 years for Ahmed's account to accumulate $500.