Given Information:
Mean time to finish 400 meter dash = μ = 65 seconds
Standard deviation to finish 400 meter dash = σ = 2.5 seconds
Confidence level = 95%
Required Information:
95% confidence interval = ?
Answer:
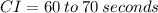
Step-by-step explanation:
In the normal distribution, the empirical rule states approximately 68% of all the data lie within 1 standard deviation from the mean, approximately 95% of all the data lie within 2 standard deviations from the mean and approximately 99.7% of all the data lie within 3 standard deviations from the mean.
The confidence interval for 95% confidence limit is given by
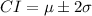
Since approximately 95% of all the data lie within 2 standard deviations from the mean. μ is the mean time Carson takes to finish 400 meter dash and σ is the standard deviation.

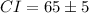
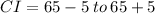
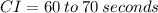
Therefore, the 95% confidence interval is between 60 to 70 seconds
What does it mean?
It means that we are 95% confident that the Carson's mean to finish 400 meter dash is within the interval of (60, 70).