Given↷
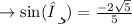
To find↷
Answer↷
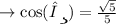
Solution↷
We know that,
sine is the ratio of adjacent side over the hypotenuse.
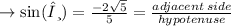
also,
cosine is the ratio of base over the hypotenuse.
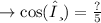
- base = √(h²-a²)
- h= hypotenuse
- a= adjacent side
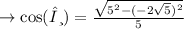
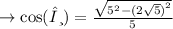
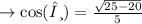
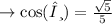
since ,cosine is always positive in the quadrant IV, option 3rd =√5/5 is correct ✓