Question

Please help me with this algebra question please u need help

Answer 1

Note:-

★theta to be used as A

`\\ \rm\Rrightarrow sinA=(-2√(5))/(5)`

Now

• cosA=1-sin²A

`\\ \rm\Rrightarrow cosA=\sqrt{1-(dfrac{-2√(5)}{5})^2}`

`\\ \rm\Rrightarrow cosA=\sqrt{1-(20)/(25)}`

`\\ \rm\Rrightarrow cosA=\sqrt{(25-20)/(25)}`

`\\ \rm\Rrightarrow cosA=(√(5))/(5)`

Option C

Answer 2

Given↷

`\huge\rightarrow\sin( θ ) = ( - 2 √(5) )/(5)`

To find↷

• cos(θ) in IV quadrant

Answer↷

`\huge\rightarrow\cos( θ ) = ( √(5) )/(5)`

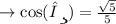
Solution↷

We know that,

sine is the ratio of adjacent side over the hypotenuse.

`\rightarrow\sin( θ ) = ( - 2 √(5) )/(5) = (adjacent \: side)/(hypotenuse) \\`

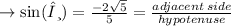
also,

cosine is the ratio of base over the hypotenuse.

`\rightarrow\cos( θ ) = (?)/(5) \\`

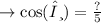
• base = √(h²-a²)
• h= hypotenuse
• a= adjacent side

`\rightarrow\cos( θ ) = \frac{ \sqrt{ {5}^(2) - ( - 2√( 5) {}^{} ) {}^(2) } }{5} \\`

`\rightarrow\cos( θ ) = \frac{ \sqrt{ {5}^(2) - {(2√( 5))}^(2) } }{5} \\`

`\rightarrow\cos( θ ) = ( √(25 - 20) )/(5) \\`

`\rightarrow\cos( θ ) = ( √(5) )/(5) \\`

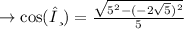
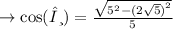
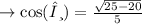
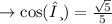
since ,cosine is always positive in the quadrant IV, option 3rd =√5/5 is correct ✓