Question

Gary Oak is on a mission to complete his Pokedex before Ash Ketchum. To this end, he starts searching the tall grass for Pokemon. Assume that there are m Pokemon in total and that Gary has seen none of them at the start. Assume also, that all of the m Pokemon are equally likely to appear in the tall grass and each appearance is independent of the previous appearances. Let K be the number of encounters required for Gary to fill his Pokedex (A filled Pokedex means that he has seen all m Pokemon atleast once). Find the expectation and variance of K.

Answer 1

i got this completely wrong cause im just gonna say the answer is pikachu

but really quick gary never sees all of the pokemon

Answer 2

Let
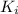`K_i` denote the number of encounters required to see a new Pokemon after having encountered
`i-1` of them. Then
`K_1=1`.

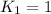If Gary has already seen
`i-1` Pokemon, that leaves
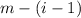`m-(i-1)` still to be encountered, and the next new encounter has a probability of
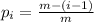`p_i=\frac{m-(i-1)}m` of occurring. Then
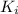`K_i` is geometric, with PMF

`P(K_i=k)=\begin{cases}(1-p_i)^(k-1)p_i&\text{for }k\ge1\\0&\text{otherwise}\end{cases}`

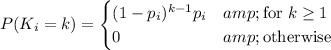
Then the expectation and variance of
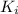`K_i` are

`E[K_i]=\frac1{p_i}=\frac m{m-(i-1)}`

`V[K_i]=\frac{1-p_i}{{p_i}^2}=(m(i-1))/((m-(i-1))^2)`

`K` is the total number of encounters needed to record all
`m` Pokemon, so

`K=\displaystyle\sum_(i=1)^mK_i`

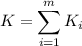
By linearity of expectation,

`E[K]=\displaystyle\sum_(i=1)^mE[K_i]=\sum_(i=1)^m\frac m{m-(i-1)}=\frac mm+\frac m{m-1}+\frac m{m-2}+\cdots+\frac m1`

`E[K]=m\displaystyle\sum_(i=1)^m\frac1i`

The
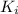`K_i` are independent, so the variance is

`V[K]=\displaystyle\sum_(i=1)^mV[K_i]=\sum_(i=1)^m(m(i-1))/((m-(i-1))^2)`

`V[K]=m\displaystyle\sum_(i=0)^(m-1)\frac i{(m-i)^2}`