Let
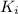 denote the number of encounters required to see a new Pokemon after having encountered
denote the number of encounters required to see a new Pokemon after having encountered
 of them. Then
of them. Then
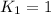 .
.
If Gary has already seen
 Pokemon, that leaves
Pokemon, that leaves
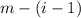 still to be encountered, and the next new encounter has a probability of
still to be encountered, and the next new encounter has a probability of
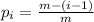 of occurring. Then
of occurring. Then
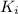 is geometric, with PMF
is geometric, with PMF
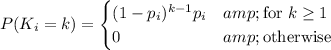
Then the expectation and variance of
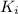 are
are
![E[K_i]=\frac1{p_i}=\frac m{m-(i-1)}](https://img.qammunity.org/2021/formulas/mathematics/college/udq9l0vtinlte4jzgnf24pazj5zrrnlp80.png)
![V[K_i]=\frac{1-p_i}{{p_i}^2}=(m(i-1))/((m-(i-1))^2)](https://img.qammunity.org/2021/formulas/mathematics/college/3746mtmfewe2syfxeqzyzpy2edgzdf6oiw.png)
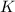 is the total number of encounters needed to record all
is the total number of encounters needed to record all
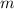 Pokemon, so
Pokemon, so
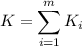
By linearity of expectation,
![E[K]=\displaystyle\sum_(i=1)^mE[K_i]=\sum_(i=1)^m\frac m{m-(i-1)}=\frac mm+\frac m{m-1}+\frac m{m-2}+\cdots+\frac m1](https://img.qammunity.org/2021/formulas/mathematics/college/o11tsp9rx25ysihq3txmomkxstkvn3vaq0.png)
![E[K]=m\displaystyle\sum_(i=1)^m\frac1i](https://img.qammunity.org/2021/formulas/mathematics/college/oe2drw472aur2kfczkn9zcc52jce4qhrp4.png)
The
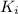 are independent, so the variance is
are independent, so the variance is
![V[K]=\displaystyle\sum_(i=1)^mV[K_i]=\sum_(i=1)^m(m(i-1))/((m-(i-1))^2)](https://img.qammunity.org/2021/formulas/mathematics/college/bm3s47s4fg1r2a3xggi4zpgqe7e3v4jqnu.png)
![V[K]=m\displaystyle\sum_(i=0)^(m-1)\frac i{(m-i)^2}](https://img.qammunity.org/2021/formulas/mathematics/college/sdglr9acwusg9jwvetfv4iyj6h15e3umpy.png)