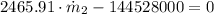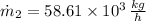Answer:
a)
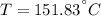 , b)
, b)
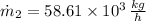
Step-by-step explanation:
A feedwater heater is a mixing chamber that pre-heats water prior to compressor, improving the efficiency of the power cycle. This system is modelled after the First Law of Thermodynamics:

The properties at inlets and outlets are, respectively:
Inlet 1 (Subcooled Liquid)
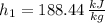
Inlet 2 (Superheated Vapor)
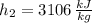
Outlet 3 (Saturated Liquid)
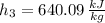
a) The temperature at the exit is:
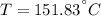
b) The mass flow rate at inlet 2 is: