To write something in slope-intercept form
⇒ need to know what slope-intercept looks like:
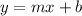
- m: the value of the slope
- b: y-intercept
Let us first find the slope:
Formula of slope =
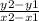
- (x1,y1): (5,6)
- (x2,y2): (8,4)
Slope =
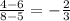
Lets now write in point-slope form:
⇒
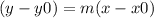
- (x0,y0): any point on the line --> (5,6)
- m: value of slope
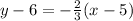
To write it into slope-intercept form, we must solve for y
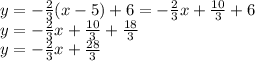 <-- slope-intercept form
<-- slope-intercept form
Hope that helps!