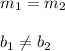Question

¿Qué pasa cuando nos enfrentamos con dos incógnitas, en el caso de que las ecuaciones que se generen sean de primer grado y formen un sistema de ecuaciones?

Answer 1

Explicación:

Una ecuación de primer grado es una ecuación lineal en la que se ven involucradas una o más variables, sin existir productos entre ellas. Por ejemplo, una ecuación de primer grado con dos incógnitas es:

`y=mx+b \\ \\m:pendiente \\ \\ b:y-intercept`

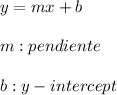
De manera que un sistema de ecuaciones con dos incógnitas podría ser:

`y=m_(1)x+b_(1) \\ \\ y=m_(2)x+b_(2)`

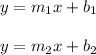
que representan ecuaciones de rectas.

Existen tres posibilidades:

1. Una solución:

Ocurre cuando las rectas no son paralelas, es decir:

`m_(1)\\eq m_(2)`

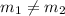
Entonces la solución es la intersección de estas dos rectas.

2. Infinitas soluciones:

Ocurre cuando las ecuaciones son las mismas, en cuyo caso las rectas son las mismas y se intersectan en todos los puntos, es decir:

`m_(1)=m_(2) \\ \\ b_(1)=b_(2)`

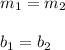
3. Ninguna solución:

Ocurre cuando las rectas son paralelas pero tienen distinta intersección con el eje y, es decir:

`m_(1)=m_(2) \\ \\ b_(1)\\eq b_(2)`