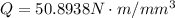Answer:
a
The volume rate of metal removed
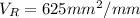
b
The number of chips formed per unit time
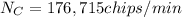
c
The average volume per chip
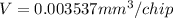
d
The the specific energy in this operation
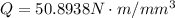
Step-by-step explanation:
From the question we are told that
The outside radius is
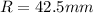
The grinding wheel diameter is
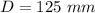
The grinding wheel width is
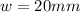
The surface speed of the work piece rotation of
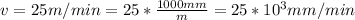
The speed of rotation of the wheel is
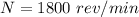
The depth of cut is
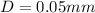
The transverse feed is

The number of
 of wheel surface is
of wheel surface is
![C = 50\ grits/cm^2 = 50 * [(10^(-2) cm )/(mm^2) ] = 50 *10^(-2) grits/mm^2](https://img.qammunity.org/2021/formulas/engineering/college/haahajsqyfx9m0sovvwkislzs1r1tcpmzf.png)
The cutting force is F = 45 N
The volume rate of the metal removed is mathematically represented as
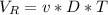
Substitution value
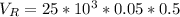
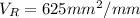
The speed of the wheel is mathematically represented


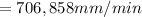
The number of chips formed per unit time is mathematically represented as
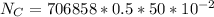
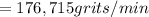
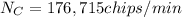
The average volume per is mathematically represented as
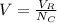
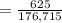
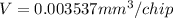
The specific energy is the operation mathematically
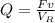
![= ((45)[ (706,858.3) * (1m)/(1000mmm) ])/(625)](https://img.qammunity.org/2021/formulas/engineering/college/weyxs27oa7qs14qey5xhzwv2qqkpzguid1.png)