Question

Which function represents a reflection of f(x) = Three-eighths(4)x across the y-axis?

g(x) = NegativeThree-eighths (one-fourth) Superscript x
g(x) = Negative three-eighths(4)x
g(x) = Eight-thirds(4)-x
g(x) = Three-eighths(4)–x

Answer 1

I got D on Edge 2020

Explanation:

Hope this helps you, have a nice day!

Answer 2

Given:

The given function is
`f(x)=(3)/(8)(4)^x`

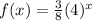
The function f(x) is reflected across the y - axis.

We need to determine the function g(x) that represents the reflection of f(x).

Function g(x):

Let us determine the function g(x).

If the function is reflected across the y - axis, then the reflected function becomes g(x) = f(-x)

Thus, applying the rule, we have;

`g(x)=(3)/(8)(4)^(-x)`

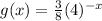
Thus, the reflection of the function f(x) across the y - axis is
`g(x)=(3)/(8)(4)^(-x)`

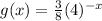
Hence, Option d is the correct answer.