Given:
The given function is
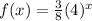
The function f(x) is reflected across the y - axis.
We need to determine the function g(x) that represents the reflection of f(x).
Function g(x):
Let us determine the function g(x).
If the function is reflected across the y - axis, then the reflected function becomes g(x) = f(-x)
Thus, applying the rule, we have;
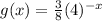
Thus, the reflection of the function f(x) across the y - axis is
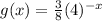
Hence, Option d is the correct answer.